How to create a random library for an specific function

[andre_fermart]

Dear experts,

I am working with a probability density function (PDF), that I named as "Jaya", as below:

f(x) = scale**(shape-1) * x**(-shape)*(np.exp(-scale/x)) / math.factorial(shape - 2)

I would like to know how can I create a function to generate random number based on the above PDF.

One example is the numpy.random.gamma that follows the Gamma PDF as below.

f(x) = x**(shape-1)*(np.exp(-bins/scale) / (sps.gamma(shape)*scale**shape))

import numpy as np
import matplotlib.pyplot as plt
import scipy.special as sps
import math


shape, scale = 3, 10**-6. 
s = np.random.gamma(shape, scale, 1000)


count, bins, ignored = plt.hist(s, 50, density=True)

#____________Gamma
y = bins**(shape-1)*(np.exp(-bins/scale) /
                     (sps.gamma(shape)*scale**shape))
plt.plot(bins, y, linewidth=2, color='r')
plt.show()

#____________Jaya
y = scale**(shape-1) * bins**(-shape)*(np.exp(-scale/bins)) / math.factorial(shape - 2)
plt.plot(bins, y, linewidth=1, color='r')
plt.show()

Thank you!

[scidam]

Lets start with creation a class that describes uniform distribution on (a_, b_) interval.

class cdist_ab(rv_continuous):   
    """Just for testing purposes: uniform distribution on (a_, b_) interval
    """ 

    def __init__(self, *args, **kwargs):
        self.a_ = kwargs.pop('a_', 0)
        self.b_ = kwargs.pop('b_', 1)
        super().__init__(self, *args, **kwargs)

    def _pdf(self, x):
        return 1/(self.b_ - self.a_) if self.a_ < x < self.b_ else 0

It seems to work fine, I just generated an array of random values:

custom_producer  = cdist_ab(a_=1, b_=5)
print(custom_producer.rvs(size=10))

Output:
[1.95859517 4.86153241 3.30723219 3.17119599 4.95076874 1.58307715
 3.93760346 3.11630877 1.8845758  3.81034867]

In case of your "Jaya" distribution we need to be sure that the pdf meets several conditions, e.g. area under (AUC) the curve is 1.0, its values at +infinity and -infinity points are zeros, etc. Nevertheless, we can try:

class cdist(rv_continuous):   # custom distribution => cdist  (don't mix with cdist helper function from spatial subpackage)
    """Custom distribution
    """ 

    def __init__(self, *args, **kwargs):
        self.scale_ = kwargs.pop('scale_', 1) # you need to provide some default parameters of the distribution
        self.shape_ = kwargs.pop('shape_', 5)
        super().__init__(self, *args, **kwargs)

    def _pdf(self, x):
        scale  = self.scale_
        shape = self.shape_
        y = scale**(shape-1) * x**(-shape)*(np.exp(-scale/x)) / math.factorial(shape - 2) 
        # you can use gamma function instead of factorial, gamma would be faster, i think
        return y

custom_producer  = cdist(shape_=2, scale_=5)
print(custom_producer.rvs(size=1))

I got this:

Output:
[-9.70220121]

Hope that helps...

[andre_fermart]

Lets start with creation a class that describes uniform distribution on (a_, b_) interval.

class cdist_ab(rv_continuous):   
    """Just for testing purposes: uniform distribution on (a_, b_) interval
    """ 

    def __init__(self, *args, **kwargs):
        self.a_ = kwargs.pop('a_', 0)
        self.b_ = kwargs.pop('b_', 1)
        super().__init__(self, *args, **kwargs)

    def _pdf(self, x):
        return 1/(self.b_ - self.a_) if self.a_ < x < self.b_ else 0

It seems to work fine, I just generated an array of random values:

custom_producer  = cdist_ab(a_=1, b_=5)
print(custom_producer.rvs(size=10))

Output:
[1.95859517 4.86153241 3.30723219 3.17119599 4.95076874 1.58307715
 3.93760346 3.11630877 1.8845758  3.81034867]

In case of your "Jaya" distribution we need to be sure that the pdf meets several conditions, e.g. area under (AUC) the curve is 1.0, its values at +infinity and -infinity points are zeros, etc. Nevertheless, we can try:

class cdist(rv_continuous):   # custom distribution => cdist  (don't mix with cdist helper function from spatial subpackage)
    """Custom distribution
    """ 

    def __init__(self, *args, **kwargs):
        self.scale_ = kwargs.pop('scale_', 1) # you need to provide some default parameters of the distribution
        self.shape_ = kwargs.pop('shape_', 5)
        super().__init__(self, *args, **kwargs)

    def _pdf(self, x):
        scale  = self.scale_
        shape = self.shape_
        y = scale**(shape-1) * x**(-shape)*(np.exp(-scale/x)) / math.factorial(shape - 2) 
        # you can use gamma function instead of factorial, gamma would be faster, i think
        return y

custom_producer  = cdist(shape_=2, scale_=5)
print(custom_producer.rvs(size=1))

I got this:

Output:
[-9.70220121]

Hope that helps...

Dear,

Thank you very much!

It help me a lot, I spend some time to learning with your script. I am still searching and learning on it.

However, I played with it in order to learn and in the code below I changed y for the gamma PDF, however something is wrong as the result is not the same as np.random.gamma

import numpy as np
from scipy.stats import rv_continuous
import matplotlib.pyplot as plt
import scipy.special as sps

class cdist(rv_continuous):   
    """Custom distribution
    """ 
 
    def __init__(self, *args, **kwargs):
        self.scale_ = kwargs.pop('scale_', 10**-6) # Why there is two lines to insert shape and scale?
        self.shape_ = kwargs.pop('shape_', 3)
        super().__init__(self, *args, **kwargs)
 
    def _pdf(self, x):
        scale  = self.scale_
        shape = self.shape_
        y = x**(shape-1)*(np.exp(-x/scale) / (sps.gamma(shape)*scale**shape)) 
        # I've changed the y for the gamma PDF
        return y

custom_producer  = cdist(shape_=3, scale_=10**-6)
a = (custom_producer.rvs(size=10))
print (a)

#____________Gamma by Numpy

shape, scale = 3, 10**-6. 
s = np.random.gamma(shape, scale, 100)

count, bins, ignored = plt.hist(s, 50, density=True)
y = bins**(shape-1)*(np.exp(-bins/scale) / (sps.gamma(shape)*scale**shape))
plt.plot(bins, y, linewidth=2, color='r')
plt.show()

Also, I got this message

Output:
IntegrationWarning: The occurrence of roundoff error is detected, which prevents 
  the requested tolerance from being achieved.  The error may be 
  underestimated.
  warnings.warn(msg, IntegrationWarning)
C:\Users\19523350\AppData\Local\Continuum\anaconda3\lib\site-packages\numpy\lib\function_base.py:2048: RuntimeWarning: invalid value encountered in ? (vectorized)
  outputs = ufunc(*inputs)
C:\Users\19523350\AppData\Local\Continuum\anaconda3\lib\site-packages\scipy\integrate\quadpack.py:385: IntegrationWarning: The maximum number of subdivisions (50) has been achieved.
  If increasing the limit yields no improvement it is advised to analyze 
  the integrand in order to determine the difficulties.  If the position of a 
  local difficulty can be determined (singularity, discontinuity) one will 
  probably gain from splitting up the interval and calling the integrator 
  on the subranges.  Perhaps a special-purpose integrator should be used.
  warnings.warn(msg, IntegrationWarning)

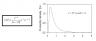
The Jaya function and graph is attached as image. In order to compare, I changed the in the code the scale to 10**-6 and the shape to 3.

[scidam]

If we consider source code of distributions.py, we can find that rv_continous class uses numerical differentiation/integration if only
few methods were defined to describe probability distribution. E.g. if we define only _pdf method, all other methods, such as .cdf, becomes defined due to machinery in rv_continous (but this machinery is numerical); So, it is better to define (override) other methods, such as ._cdf, ._icdf explicitly; If these methods are defined explicitly, no numerical differentiaion/integration or other complex stuff be applied; Therefore, it is better to define as many helpers ._pdf, _cdf etc. as possible. This will increase speed and reliability of further computations. In our case, we define ._pdf only... What is .rvs? .rvs is based on uniform distribution on [0,1) and inverse cdf; if you didn't define inverse cdf explicitly for your distribution, rv_continous class tries to do all work numerically (numerical approach is less robust than computing analytical formula of icdf). This is why some warnings or even errors can occur.
I just replaced return y with return y if x>0 else 0.0 and tried to call .rvs (parameters were shape_=3, scale_=1): everything went fine. So, what to do?! You need to generate random numbers from Jaya distribution, ok. You can drop using rv_continous at all. Look at implementation of _rvs method and, if you know inverse cdf of the distribution, just generate uniformly distributed values in [0,1) and apply inverse cdf to them and you get values that have specific distribution.
So, is it possible to find analytical forms of cdf or better inverse cdf for Jaya distribution? This is the question to be investigated.

[andre_fermart]

If we consider source code of distributions.py, we can find that rv_continous class uses numerical differentiation/integration if only
few methods were defined to describe probability distribution. E.g. if we define only _pdf method, all other methods, such as .cdf, becomes defined due to machinery in rv_continous (but this machinery is numerical); So, it is better to define (override) other methods, such as ._cdf, ._icdf explicitly; If these methods are defined explicitly, no numerical differentiaion/integration or other complex stuff be applied; Therefore, it is better to define as many helpers ._pdf, _cdf etc. as possible. This will increase speed and reliability of further computations. In our case, we define ._pdf only... What is .rvs? .rvs is based on uniform distribution on [0,1) and inverse cdf; if you didn't define inverse cdf explicitly for your distribution, rv_continous class tries to do all work numerically (numerical approach is less robust than computing analytical formula of icdf). This is why some warnings or even errors can occur.
I just replaced return y with return y if x>0 else 0.0 and tried to call .rvs (parameters were shape_=3, scale_=1): everything went fine. So, what to do?! You need to generate random numbers from Jaya distribution, ok. You can drop using rv_continous at all. Look at implementation of _rvs method and, if you know inverse cdf of the distribution, just generate uniformly distributed values in [0,1) and apply inverse cdf to them and you get values that have specific distribution.
So, is it possible to find analytical forms of cdf or better inverse cdf for Jaya distribution? This is the question to be investigated.

Thank you very much!!